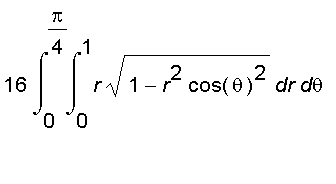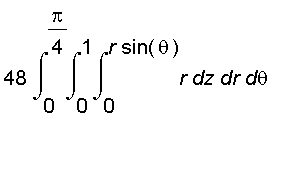¡@
Discovery Project
--- The Intersection of Three Cylinders
¡@
1.
![[Maple Plot]](images/ans_porj_cylind1.gif)
The solid enclosed by the three cylinders
,
, and
is shown above; where the green surface is the cylinder
, the blue surface is the cylinder
, and the yellow surface is the cylinder
.
¡@
¡@
2.
To find the volume, we can split the solid into sixteen congruent pieces, one of which lies in the part of the first octant with
in [0,
],as shown below.
![[Maple Plot]](images/ans_porj_cylind10.gif)
This piece is described by
{ (
,
,
) |
and
,
and
,
and
}.
So the volume of the solid is
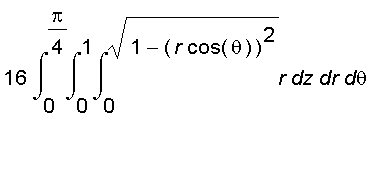
=
=
.
we can also split the solid into forty eight congruent pieces as follows :
![[Maple Plot]](images/ans_porj_cylind23.gif)
One of the piece which lies in the part of the first octant is shown below.
![[Maple Plot]](images/ans_porj_cylind24.gif)
This piece is described by
{ (
,
,
) |
and
,
and
,
and
}.
So the volume of the solid is
=
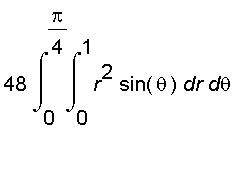
=
=
.
¡@
3.
One possible set of parametric equations ( with all sign choices allowed ) of the edges of the solid is
,
or
,
or
for all
in [
,
] .
or
,
or
,
for all
in [
,
] .
or
,
,
or
for all
in [
,
] .
![[Maple Plot]](images/ans_porj_cylind62.gif)
¡@
4. Let the three cylinder be
,
, and
.
(a) If
, the four faces in problem 1 collapse into a single face, as in the graph below.
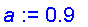
![[Maple Plot]](images/ans_porj_cylind68.gif)
(b) If
<
<
, then each pair of vertical opposite faces, defined by one of the other two cylinders, collapse into a single face. The graph of the case for
is shown below.
![[Maple Plot]](images/ans_porj_cylind73.gif)
(c) If
, then the solid of intersection coincides with the solid of intersection of the two cylinder
, and
, as in the graph below, where the blue surface is the cylinder
, and the green surface is the cylinder
.
![[Maple Plot]](images/ans_porj_cylind79.gif)
5.
(a) If
, we split the solid into sixteen congruent pieces, one of which can be described as the solid above the polar region
{ (
,
) |
and
,
and
}
in the xy-plane and below the surface
, as shown below.
![[Maple Plot]](images/ans_porj_cylind88.gif)
Thus, the total volume is
.
(b) If
<
<
, we split the solid into sixteen congruent pieces, one of which is the solid above the regions
,
and below the surface
, where
is the right triangular region
{ (
,
) |
and
,
and
} ,
and
is the circular polar region
{ (
,
) |
and
,
and
} .
( as the figure below).
![[Maple Plot]](images/ans_porj_cylind110.gif)
![[Maple Plot]](images/ans_porj_cylind111.gif)
Using rectangular coordinates for the region
and polar coordinates for the region
, we find the total volume of the solid to be
+
.
¡@
(c) If
, we split the solid into sixteen congruent pieces, one of which can be described as the solid above the region { (
,
) |
and
,
and
} in the xy -plane and below the surface
,as shown below.
![[Maple Plot]](images/ans_porj_cylind124.gif)
Thus, the total volume is
.